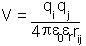
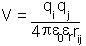
The strictly correct way to use the law would be to consider every nucleus and electron separately, plug it into the Schrödinger equation and apply quantum chemical methods to solve the equation for the spatial configuration of nuclei we are interested. As already mentioned this is completely impractical for biomolecular systems. So instead we wish to develop a useful model for the interactions between nuclear centres (commonly called "atoms") without having to explicitly deal with the electrons in a system.
and
- magnitude of the charges,
- their separation
the permittivity of free space
the relative dielectric constant of the medium in which the charges are placed
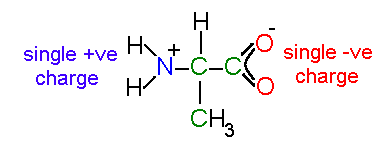
an isolated alanine residue in solution
Note that the atoms in a charged carboxylic acid are equivalent - the
double bond is delocalized across the group.
In proteins the individual amino acids are polymerized.
This results in a peptide backbone which is electrically neutral with the exceptions of the ends of the chain.
In a normal protein the amino end carries a positive charge (-NH2+) and the carboxyl end carries a negative charge (-CO2-).
In some cases (e.g., a number membrane polypeptides) the ends are chemically modified to avoid these charges (for instance by acetylation of the amino end group).
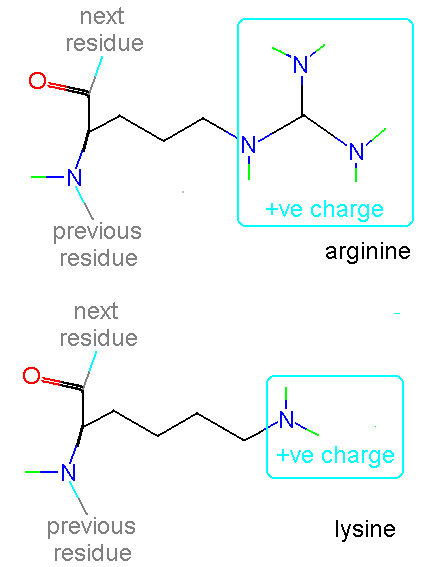
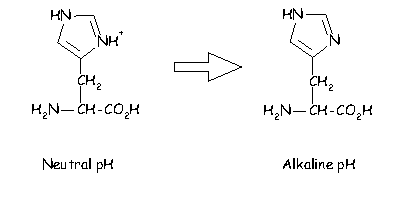
In addition histidine is normally charged at neutral pH (the charge normally residing on the delta carbon but sometimes on the epsilon). When the residue is placed in a basic environment it loses a proton and becomes uncharged:
Very many proteins bind inorganic ionic species such as metal ions - indeed such ions can play a crucial role in the mechanism of a protein. An example of this is the enzyme xylose isomerase which has two Mg2+ ions at the active site which coordinate to the substrate, polarizing it and stabilizing the transition state in the reaction.
Click here
if
you would like to see an example of a salt bridge.
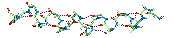click to see larger picture
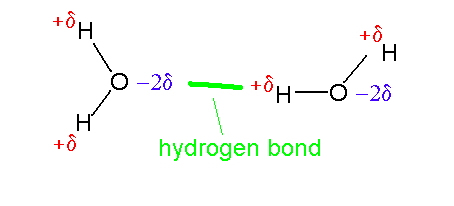
click to see larger pictureNote that under aqueous conditions the main chain carbonyl and amino groups are stabilized by hydrogen bonds to water even in the unfolded (random coil) state. In the folded state these groups are almost invariably involved in hydrogen bonds but overall there is normally a slight destabilization in comparison to the random coil (proteins have marginal stability due to effects such as the hydrophobic effect).
The most common approach is to place a partial charge at each atomic centre (nucleus). These charges then interact by Coulomb's Law. The charge can take fractions of an electron and can be positive or negative. Charges on adjacent atoms (joined by one or two covalent) bonds are normally made invisible to one another - the interactions between these atoms being dealt with by covalent interactions. Note that the concept of a partial charge is only a convenient abstraction of reality. In practice many electrons and nuclei come together to form a molecule - partial charges give a crude representation of what a neighbouring atom will on average "see" due to this collection.
The standard modern way to calculate partial charges is to perform a (reasonably high level) quantum chemical calculation for a small molecule which is representative of the group of interest (e.g., phenol is considered for tyrosine). The electrostatic potential is then calculated from the orbitals obtained for many points on the molecular surface. A least squares fitting procedure is then used to produce a set of partial charges which produce potential values most consistent with the quantum calculations. (Cieplak, P., Cornell, W.D., Bayly, C., Kollman, P.A. (1995) application of the multimolecule and multiconformational RESP methodology to biopolymers - charge derivation for DNA, RNA and proteins. J. Comp. Chem. 16:1357-1377). Older procedures used methods in which orbital populations are simply split between atoms (Mulliken Population Analysis). All though much simpler these charges do not produce a reasonable representation of the electrostatic potential around a molecule - which is usually what is of interest in a simulation.
To see the kind of values typical for partial charges look at
picture
of a salt bridge.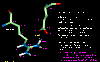
As mentioned previously using partial charges at nuclear centres is the crudest effective abstraction. To obtain a more accurate representation two approaches are common. The first is to add dipole, quadrapole and higher moments to the nuclear centres (do not worry if these terms are unfamiliar, see: Stone, A.J., Price, S.L. (1988) Some ideas in the theory of intermolecular forces: Anisotropic atom-atom potentials. J. Phys. Chem. 92:3325-3335). The second is to introduce further non-nuclear centres - this is commonly done to represent the anisotropy in potential cause by lone pairs on oxygen atoms (Cieplak, P., Cornell, W.D., Bayly, C., Kollman, P.A. (1995) application of the multimolecule and multiconformational RESP methodology to biopolymers - charge derivation for DNA, RNA and proteins. J. Comp. Chem. 16:1357-1377).
In many respects electrostatic interactions provided the biggest problems
to computational studies of protein behaviour. By their nature they are
long range and dependent on the properties of the surrounding medium (see
discussion of dielectric
effects). A simple rule of thumb is that the more highly charged a
system the harder it is to simulate - thus simulations of liquid argon
can do a wonderful job, hydrocarbons are fairly easy, water becomes difficult
and proteins more so. The limit is reached with nucleic acids like DNA
which are aqueous complex salts (each base having a charge of minus two)
with counter ions and solvent having important effects on structures. Usually
some sort of "fudge" has to be made in simulations to keep DNA stable at
all!
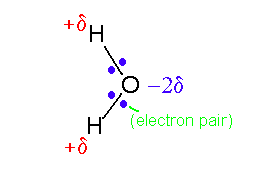
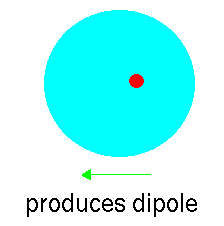
Imagine that we have an atom of argon. It can be considered to be like
a large spherical jelly with a golf ball embedded at the centre. The golf
ball is the nucleus carrying a large positive charge and the jelly represents
the clouds of electrons whizzing about this. At a point external to the
atom the net average field will be zero because the positively-charged
nucleus' field will be exactly balanced by the electron clouds:
However, atoms vibrate (even at 0K) and so that at any instant the
cloud is likely to be slightly off centre. This disparity creates an "instantaneous
dipole":
Suppose that we have another argon atom close to the first. This atom
will see the electric field resulting from the instantaneous dipole. This
field will effect the jelly inducing a dipole:
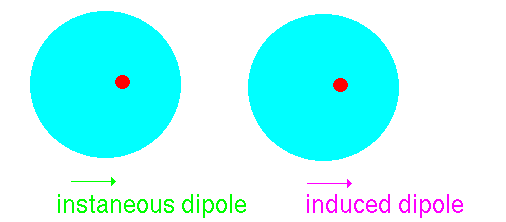
The two dipoles attract one another - producing an attractive interaction.
The Dispersion interaction can be shown to vary according to the inverse sixth power of the distance between the two atoms:
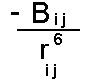
The factor Bij
depends on the nature of the pair of atoms interacting (in particular their polarizability). It is normal to parameterize the dispersion empirically using structural and energetic data from crystals of small molecules. It is not possible to use simple quantum chemical calculations to find parameters. This is because most quantum chemical calculations use the self consistent field approximation (SCF). In this each electron is solved independently keeping the other orbitals frozen (in a self consistency). This effectively means that electrons only experience a time averaged picture of other electrons - so that dispersion cannot come into effect. More advanced methods in quantum chemistry introduce methods to tackle "electron correlation" to avoid this problem.
The simplest and oldest way to represent the repulsive core for atoms is by using a "hard sphere" model. In this atoms have a characteristic radius (below the van der Waals radius) and cannot overlap. This approach can be adopted computationally but is more commonly seen in physical models using plastic spheres such as CPK:
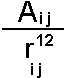
The repulsive term (it is always positive) drops away dramatically as the distance between the two atoms increases but conversely becomes very large at short distances - providing a "fuzzy" core. This is the approach normally adopted for protein potential energy functions. When more accuracy is required a two parameter model is normally adopted:
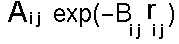
This term together with a representation for dispersion by a term in Rij-6 is commonly known as the "Buckingham potential". It provides a more realistic representation particularly at short distances where a term in R-12 is too step. It is not normally used for macromolecular applications as the increase in complexity (introduction of an additional parameter) and in computational cost (it takes a long time to calculate exponentials) is undesirable.
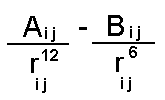
The equation can be rewritten in an equivalent more instructive form (choosing the case for an interaction between two atoms of the same type):
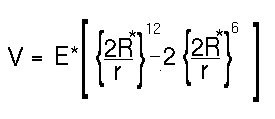
The minimum of the function is at r = 2R* and has an energy of minus E*. The distance R* is known as the van der Waals radius for an atom and E* is its van der Waals well depth. Typical values for these parameters (from the AMBER force field) are shown below.
atom type van der Waals radius van der Waals well depth in Å in kcal/mol
C (aliphatic) 1.85 0.12 O 1.60 0.20 H 1.00 0.02 N 1.75 0.16 P 2.10 0.20 S 2.00 0.20
It is important to note that the Lennard-Jones interaction between uncharged atoms (such as CH3 groups) is less attractive than that between charged groups such as oxygens. The difference is that the contribution from electrostatics will dominate the L-J interactions.
In cases where uncharged groups form compact structures van der Waals energies are often cited as stabilizing the conformation. Although partly true very often the major contribution comes rather from hydrophobic exclusion.
On to next course unit The effect of solvent and hydrophobic interactions
