Page 130 out of 225 pages in this book.
Tripos Bookshelf  >  QSAR  >  QSAR Theory  >  QSAR Techniques

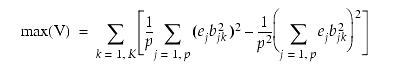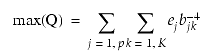
4.5.3.3 Factor Rotation

Rotation of the principal component axes can enhance their interpretability. Each principal component represents an underlying factor, which is a linear combination of the original measurements (columns of data). If all the measurements load equally onto a factor, it is difficult to interpret it from a theoretical or experimental point of view. However, if one group of variables loads heavily, say, into the first factor, and another different group into the second, the structure becomes clearer.

Put differently, when such a linear structure exists, the alignment of a coordinate system which best describes the simpler structure seems somewhat arbitrary. (In the scores plot of Figure 23, benzene could be rotated around the Z axis in any direction, yielding many different and valid X-Y coordinate sets.) The SYBYL/QSAR version of factor analysis provides three common approaches for rotating these axes. The default method used in the benzene run is principal component analysis (PCA), which is the same as no rotation. The first axis points in the direction of highest data variance, and subsequent axes are orthogonal along directions of highest remaining variance. The varimax procedure rotates the axes to maximize the variance of the scores for each given factor (the intent being to make the factors as distinctive as possible). The quartimax method tries, as much as possible, to align each loading with a factor (the intent being to align the axes with the measured input properties).

More formally, the varimax criterion is to maximize the following expression, while keeping the b values orthogonal and the communalities constant:

[EQ 16]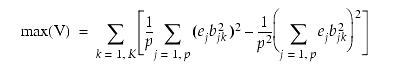

This simplifies the eigenvectors by maximizing the variance of the loadings in each factor. The quartimax criterion is to maximize the following expression, also keeping the b values orthogonal and the communalities constant:

[EQ 17]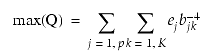

These rotation procedures simplify the loadings of a variable (column) onto the various factors by maximizing their variance. (To take a different example, if one wanted to maximize the sum of squared errors while keeping the sum of errors constant, one would assign all of the errors onto one observation while making the others zero.) Analogously, these rotations obtain the desired result, converting the loadings into more large and small ones instead of all of medium values, by maximizing these variance functions.

Note: Varimax and quartimax rotations in a factor analysis are strictly correct only when the maximum number of components (COMPONENTS 0) are used. The rotations are performed after calculating the factor matrix, but with fewer components parts of that matrix are zeroes, and thus the resulting rotations are not meaningful.