Caution: Degeneracy checking is still an experimental feature. It is designed to be used as a tool in speeding up DOCK runs involving force-field score minimization, but it can often be equally effective to use minimization without degeneracy checking with greatly reduced bin sizes.

Theory

Problem description

The tricky part of the problem is that we have to know where in the active site an orientation lies based solely on the sphere-atom pairings involved in the match; at this stage in the program we have no information of atom coordinates as the ligand has not yet been placed into the context of the receptor. Furthermore, we have to know when the same geometry has been produced with different pairings. Consider the simple model depicted below, with E being the "receptor," F the "ligand," and circled points are spheres. Using a three-node match, we can superimpose F onto E by the pairings b3, c4, d5. However, the matching of a2, e6, d5 produces the identical geometric orientation. Given the latter pairing, we must be able to recognize that this will generate an orientation degenerate with the former.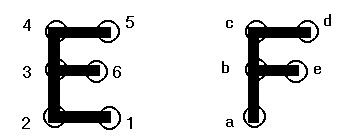


Degeneracy check

When a unique orientation is found (e.g. the very first match), the program saves the nearest sphere to every atom in the ligand - this information is, of course, dependent on the orientation relative to the receptor. Every subsequent orientation must be checked for degeneracy, i.e. has this geometry been seen before? We may only use the four sphere-atom pairings used to generate the match, otherwise we waste the time required to orient the orientation in the site and transform the coordinates (for sake of discussion, we will assume four nodes are required for a match). A simple check to see if all four pairings occurred simultaneously in a previous unique match tells us the answer. Note that we must save the nearest sphere to every atom in the ligand for unique matches to allow detection of similar geometries produced by different pairings.

Information storage

Saving a list of all matches for each possible sphere-atom pairing (maxlig (500) by maxpts (120) by at least 10,000 unique matches at 4 bytes per integer = 2.4Gb array with current dimensions) requires a tremendous amount of memory, since Fortran does not support dynamic memory allocation. Moreover, much of this array would be empty, so this is a problem that lends itself to hashing. We employ open addressing with double hashing, as per Knuth. The hash table allows us to store only non-zero elements of the 3-dimensional array mentioned earlier, with clever methods of retrieving information given a hash code. The hash code is a function of one sphere-atom pairing and dictates where in the table matches containing this pair have be found. Thus, given one sphere-atom pairing, one can quickly retrieve all other orientations which contained this pairing.

Sensitivity reduction

All that is required for differentiating orientations is a small set of way points in the active site. Here, a way point is merely a geometric descriptor which signals the occupancy by the ligand of a particular portion of the active site volume. A typical active site will be represented by on the order of 50-100 spheres, usually overkill for such a simple task. Each way point describes a particular volume within the site, this volume inversely proportional to the number of way points. A ligand orientation is described by the way points its atoms "see." The more way points one uses, the more discerning the program will be in differentiating active site volume. Rephrased, fewer degenerate orientations will be removed because more matches will be considered unique. The goal here is the opposite: to reduce the number of orientations passed through to the minimizer. We can easily reduce the number of way points by clustering the sphere set ("true spheres") to generate a reduced set of virtual spheres. All neighboring true spheres are jointly averaged into one virtual sphere. This creates an even distribution of way points throughout docking space.

Degeneracy stringency

Another method for removing more degenerate orientations is to allow some slop in comparing the sphere-atom pairings with those in unique matches. This feature is termed "wobble," as we may permit a non-zero number of "mistakes" in the degeneracy check. The predictable effect of introducing wobble is to increase the number of degenerate orientations because binding modes are smeared out over a larger volume.

Safety net

Because the first orientation in a family is deemed the representative of a particular binding mode, our depiction of this binding mode is highly dependent on the quality of the orientation. All future orientations in this family will be considered degenerate to the initial member. If the quality (e.g. force-field score) is very poor, then we unfairly represent this binding mode. It would be beneficial to afford popular binding modes renewed chances at locating an optimal representative. The parameter degenerate_save_interval dictates how often we must find a degenerate orientation in a family before orienting and minimizing another member. The degenerate_save_interval parameter has the desirable effect of smoothing our sampling over all binding modes.

Create virtual spheres as follows. Reduce the actual sphgen sphere cluster to virtual spheres by running the interactive program virtual_spheres on your sphgen sphere center file. For the intersphere cutoff distance (parameter vsph), use a value of 2.0 Å. Smaller cutoff distances have less of a reducing effect on the original sphere set than do larger cutoff distances. Having more virtual spheres (smaller cutoff distance) provides fewer degenerate orientations. Consequently, runtime will be longer but accuracy improved. Note that a file called merge.lst was created - this file lists which true sphgen spheres were averaged (merged) into which virtual sphere. View the virtual sphere PDB file on a graphics terminal to verify that they are evenly spaced at a sufficient density for your application.

An aside on the creation of virtual spheres: The vsph parameter is inversely related to the number of virtual spheres produced. The virtual spheres are used as way points within the active site for describing an orientation's location. The fewer virtual spheres, the less discriminating the algorithm can be for telling orientations apart. The extreme is having one virtual sphere, which would consider all orientations as identical and only the first match found would be minimized. Consequently, at this extreme the run-time would be the shortest as the fewest possible orientations are minimized and the results would be essentially useless. So, the trend is as follows: decreasing vsph increases the number of virtual spheres which increases the number of orientations minimized. This results in longer run-times with improved, though redundant, results. I have examined the vsph parameter over a range from 1.0 to 3.0 Å and have found that 1.5 Å and 2.0 Å provide the best results in the shortest time.

• the name of the virtual sphere file created in the previous step
• the PDB box file enclosing the active site, used with chemgrid
• the resolution of the grid (use the same as used in chemgrid)
• the prefix for chemgrid grid files

Add the check_degeneracy keyword to your INDOCK parameter file. Other parameters should be customized by using the appropriate keyword, as described below:

bin sizes

should be increased relative to a minimization with no degeneracy checking run because degeneracy checking circumvents many minimizations.

bump_maximum

should be taken under consideration. In contrast with minimization without degeneracy checking, increasing the number of bumps does not necessarily increase result quality. A bell-shaped curve is observed for "result quality" vs. number of bumps. At too few bumps, it is often the case that an orientation near the true binding mode can never be found because too few steric clashes are being allowed for minimization to resolve - the minimizer is not used to its fullest potential. At the other end of the spectrum, too many bumps allows storage of potentially terrible orientations to which other orientations will be considered degenerate - the best orientations in this binding mode will probably be thrown out.

degeneracy_wobble

dictates how stringent degeneracy checking will be. This parameter is inversely related to run-time. Higher degeneracy_wobble values permit looser degeneracy checking, resulting in more degenerate orientations and fewer orientations minimized. degeneracy_wobble of 0 is usually too stringent and run-times can become inflated. degeneracy_wobble of 2 often provides fast results of good quality.

degenerate_save_interval

specifies the number of times an orientation must be found in any given family before minimizing and attempting to save another member of the same family. So, if a particular binding mode is found 100 times and degenerate_save_interval is 25, DOCK will minimize and evaluate four additional members of this family in hopes of finding a better scoring representative. This parameter provides a method for retaining additional members of popular families and smoothing the bias of sphere locations. Recommended values are in the range 10 to 25.

check_degenerate_children

indicates whether to check for degeneracy against orientations which were saved as multiples of a family due to the degenerate_save_intervalparameter. Recommended value is off.

Cautions